When we think about numbers, we often encounter square roots as an essential mathematical concept. Square roots are intriguing and hold significant importance in various fields, including mathematics, science, engineering, and even everyday calculations. In this article, we will delve into the world of square roots and explore the square roots of numbers from 1 to 100. Let’s unlock the mystery of these roots and understand their significance.
Before we dive into specific square roots, let’s grasp the concept of square roots itself. The square root of a number is a value that, when multiplied by itself, yields the original number. For example, the square root of 4 is 2 since 2 * 2 equals 4. In mathematical terms, if “√” represents the square root, then √4 = 2.
Square Root 1 to 100
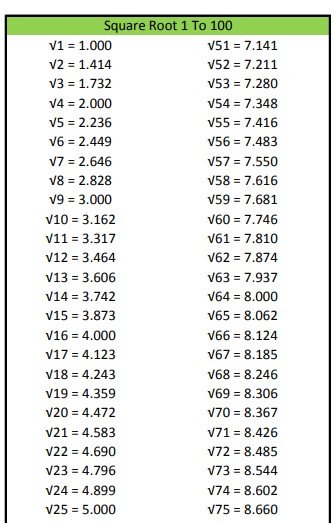
Square Root 1 to 100 Chart With Pdf Download
 Loading…
Loading…
Square Roots of Prime Numbers
Prime numbers, those divisible only by 1 and themselves, possess unique square roots:
- √2 ≈ 1.414
- √3 ≈ 1.732
- √5 ≈ 2.236
- √7 ≈ 2.646
- √11 ≈ 3.317
- √13 ≈ 3.606
- √17 ≈ 4.123
- √19 ≈ 4.359
- √23 ≈ 4.796
- √29 ≈ 5.385
The square roots of prime numbers are always irrational, and their decimal expansions go on infinitely without a repeating pattern.
Check our square root calculator
Perfect Squares and Non-Perfect Squares
Square roots can be classified into two categories: perfect squares and non-perfect squares.
- Perfect Squares: These are square roots of numbers that result in whole numbers. For example, the square root of 16 is 4, and the square root of 81 is 9.
- Non-Perfect Squares: These are square roots that result in irrational numbers, such as the square root of 2 or the square root of 10.
Square Root 1 to 100 for Perfect Squares
square root values for perfect squares from 1 to 100:
√1 = 1
√4 = 2
√9 = 3
√16 = 4
√25 = 5
√36 = 6
√49 = 7
√64 = 8
√81 = 9
√100 = 10
Square Root 1 to 100 for Non-Perfect Squares
square root values for non-perfect squares from 1 to 100:
√2 = 1.414
√3 = 1.732
√5 = 2.236
√6 = 2.449
√7 = 2.646
√8 = 2.828
√10 = 3.162
√11 = 3.317
√12 = 3.464
√13 = 3.606
√14 = 3.742
√15 = 3.873
√17 = 4.123
√18 = 4.243
√19 = 4.359
√20 = 4.472
√21 = 4.583
√22 = 4.690
√23 = 4.796
√24 = 4.899
√26 = 5.099
√27 = 5.196
√28 = 5.292
√29 = 5.385
√30 = 5.477
√31 = 5.568
√32 = 5.657
√33 = 5.745
√34 = 5.831
√35 = 5.916
√37 = 6.083
√38 = 6.164
√39 = 6.245
√40 = 6.325
√41 = 6.403
√42 = 6.481
√43 = 6.557
√44 = 6.633
√45 = 6.708
√46 = 6.782
√47 = 6.856
√48 = 6.928
√50 = 7.071
√51 = 7.141
√52 = 7.211
√53 = 7.280
√54 = 7.348
√55 = 7.416
√56 = 7.483
√57 = 7.550
√58 = 7.616
√59 = 7.681
√60 = 7.746
√61 = 7.810
√62 = 7.874
√63 = 7.937
√65 = 8.062
√66 = 8.124
√67 = 8.185
√68 = 8.246
√69 = 8.307
√70 = 8.367
√71 = 8.426
√72 = 8.485
√73 = 8.544
√74 = 8.602
√75 = 8.660
√76 = 8.718
√77 = 8.775
√78 = 8.832
√79 = 8.888
√80 = 8.944
√82 = 9.055
√83 = 9.110
√84 = 9.165
√85 = 9.220
√86 = 9.274
√87 = 9.327
√88 = 9.381
√89 = 9.434
√90 = 9.487
√91 = 9.539
√92 = 9.592
√93 = 9.644
√94 = 9.695
√95 = 9.747
√96 = 9.798
√97 = 9.849
√98 = 9.899
√99 = 9.950
How to Find Square Root from 1 to 100?
for finding the square root from 1 to 100 using two methods: the Prime Factorization Method and the Long Division Method.
Method 1: Prime Factorization Method
The prime factorization of a number means expressing that number as a product of prime numbers. To find the square root of a given number using the prime factorization method, follow these steps:
Step 1: Begin by dividing the given number into its prime factors. Step 2: Form pairs of factors where both factors in each pair are equal. Step 3: After creating pairs, take one factor from each pair. Step 4: Multiply the factors obtained by taking one factor from each pair. Step 5: The product obtained in the previous step is the square root of the given number.
Example: Find the value of √49
Solution:
The prime factorization of 49 is 7 × 7. Now, when we form pairs from the factors, we get 7. Therefore, the value of √49 = 7.
Method 2: Long Division Method
Example: Find the value of √8
Solution: Let’s find the square root of 8 using the long division method as follows:
- Start with an estimated value for the square root, for example, 2.
- Divide the number 8 by the estimated value (2) to get a quotient of 4.
- Take the average of the estimated value and the quotient (average of 2 and 4 is 3).
- Repeat the division with the new estimated value (3) and continue this process until the desired level of accuracy is achieved.
- The final value obtained after repeating the process is the square root of 8, which is approximately 2.828.
The symbol for square root (√) was first introduced by the renowned mathematician Leonhard Euler in the 18th century.
The ancient Babylonians were among the first civilizations to discover approximations for square roots.
The square root of 100 is 10, making it the largest square root among the numbers we have explored.
Square roots are fascinating mathematical entities that hold immense significance in various disciplines. From the simplicity of perfect squares to the complexity of irrational roots, they continue to play a vital role in our understanding of the world. Whether in engineering, physics, finance, or computer graphics, square roots are indispensable tools for solving practical problems and advancing our knowledge.
FAQs
- Q: Are square roots only applicable to positive numbers? A: Yes, square roots are only defined for non-negative numbers. The square root of a negative number is considered an imaginary number.
- Q: What is the square root of zero? A: The square root of zero is 0 since 0 multiplied by 0 equals 0.
- Q: Can square roots be decimal numbers? A: Yes, square roots can be decimal numbers. If the result is not a perfect square, the square root is typically an irrational decimal.
- Q: What is the square root of 50? A: The square root of 50 is approximately 7.071.
- Q: Are square roots and exponents related? A: Yes, square roots and exponents are inversely related. If “a” is a positive number, then √a is the same as raising “a” to the power of 1/2.





